Összetett feladatok
Bumm!
Kisebb gyerekek szokták játszani a Bumm! nevű társasjátékot. A játékosok 1-től kezdve egy határszámig egyesével mondják a következő számot, de az úgynevezett tiltott szám és többszörösei helyett azt kell mondani, hogy „Bumm!”. Szintén Bumm!-ot kell mondani akkor, ha a szám tartalmazza a tiltott számot számjegyként. Aki eltéveszti, zálogot ad.
Készítsünk a játék szabályainak megfelelő sorozatot!
Példa: játék 15 3 Eredmény: [1 2 Bumm! 4 5 Bumm! 7 8 Bumm! 10 11 Bumm! Bumm! 14 Bumm!]
Tessék betűzni!
A telefonban egy nehezen érthető szót betűzni szoktunk. Sokszor még így is összekeverjük a betűket. Ilyenkor a szó minden betűje helyett egy olyan szót vagy nevet mondunk, amely a megfelelő betűvel kezdődik. A nevek listában rendelkezésünkre áll az ábécé minden betűjéhez egy szó, többnyire keresztnév. Azokat az összetett betűket, amelyek nem fordulnak elő a listában, külön betűzzük.
Készítsük el egy karakteres kifejezés betűzését, azaz az ezeknek megfelelő kezdőbetűjű szavak listáját!
nevek: [Anna Ádám Bálint Cecil Dénes Ervin Éva Ferenc Gábor Hugó Ilona Ír János Kálmán László Mária Nóra Ottó Óra Ödön Őr Pál Kú Rózsi Sándor Tibor Ubul Úr Üzbég Űr Vilma Xénia Ypszilon Zoltán]
Példa: tessék "Jeromos Eredmény: [János Ervin Rózsi Ottó Mária Ottó Sándor]
Római szám átváltása tízes számrendszerbe
A következő feladatokban csak a nagybetűs, 1-től 4000-ig terjedő római számokkal foglalkozunk. A római számjegyek értékei:
| Római számjegyek jelei |
Érték |
I |
1 |
V |
5 |
X |
10 |
L |
50 |
C |
100 |
D |
500 |
M |
1000 |
Alakítsuk át a római számokat tízes számrendszerbe! (A számok helyességének vizsgálata nem feladat.)
Példa:
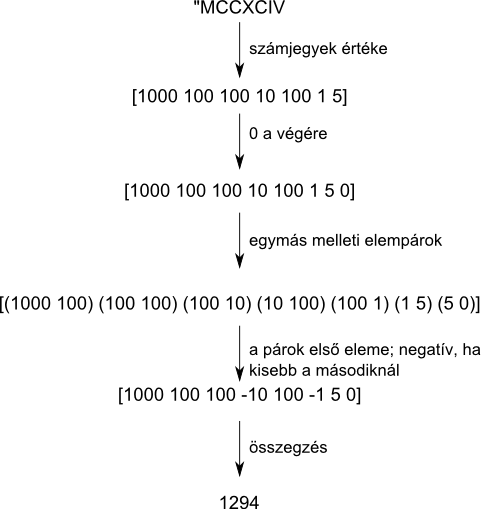
római_tízes "MCCXCIV Eredmény: 1294
római_tízes "MMIX Eredmény: 2009
Megoldás algoritmusa:
Személyi szám
A közigazgatási rendszerben használt személyi azonosító (személyi szám) több információt tárol. Az azonosító szám felépítése a születés időpontjától függ. Használatát és képzési szabályát törvény írja elő, amely 1997. január 1-jével és 2000. január 1-jével változott:
„1. A személyi azonosító tizenegy jegyű szám.
2. A személyi azonosítót az alábbiak szerint kell képezni:
a) az 1. számjegy az állampolgár születésének évszázadát és nemét jelöli a következők szerint:
1997. január 1. és 1999. december 31. között született férfi 1; nő 2 és 1999. december 31. után férfi 3; nő 4.
b) a 2-7. számjegyek a polgár születési évének utolsó két számjegyét, a születés hónapját és napját tartalmazzák;
c) a 8-10. számjegyek az azonos napon születettek születési sorszáma;
d) a 11. számjegy az 1-10. számjegyek felhasználásával, matematikai módszerekkel képzett ellenőrzőszám.
3. A személyi azonosító 11. számjegyét úgy kell képezni, hogy a 2. a)-c) pontok szerint képzett számjegy mindegyikét meg kell szorozni egy számmal, mégpedig a 10. helyen állót eggyel, a 9. helyen állót kettővel és így tovább. A szorzatokat össze kell adni, és az összeget tizeneggyel elosztani. A 2. c) pont szerinti születési sorszám nem osztható ki, ha a tizeneggyel való osztás maradéka egyenlő tízzel.”
Készítsünk függvényeket egy tetszőlegesen begépelt személyi szám információtartalmának megjelenítésére!
Példa:
személyiszám 40504291247 Eredmény: Ellenőrzés: igaz Neme: nő Születés_év: 2005 Hó: 04 Nap: 29 Sorszám: 124
Sportlövészet
A sportlövő edzéseken a hagyományos lőfegyvereken kívül elektronikus változatokat is használnak. A lőállásokból ekkor monitorokon szimulált lőlapokra történik a „tüzelés”. Elektronikus rendszer tárolja a lövések koordinátáit és értékeli ki az eredményeket.
A céltábla a koordinátarendszerében rögzítésre kerülnek a versenyző lövéseinek (x,y) vízszintes és függőleges koordi-nátái. A kiértékeléshez a találatok körértékét számolják ki. Ennek szabályai a következők:
- A lövés a maximális 10 kört éri, ha a céltábla közepébe talált. Az érték annyival csökken, ahány egységgel messzebb van a középponttól:
$
~É=10~-~\sqrt{x^2~+~y^2}
$
- Ha a találat a középponttól 10-nél nagyobb távolságra van, akkor a körérték 0.
- A körértéket végül két tizedesre kerekítik.
A versenyző egyes találatainak koordinátái a következő listában olvashatók.
Például:
[[-5,28 -1,42] [6,17 18,67] [1,50 3,07] [-0,36 -0,78] [-6,65 -8,04] [-3,00 -8,41] [6,07 0,22]]
A példa jelentése:
- Az első találat körértéke tehát
$
10~-~\sqrt{(-5,28)^2~+~(-1,42)^2}~=~4,53
$.
- A második találat körértéke 0.
Készítsük el az alábbi problémák megoldását:
- Állítsuk elő találatok körértékének sorozatát! (körérték :l)
- Listázza ki a legnagyobb találat sorszámát és körértékét! (lőmax :l)
- A célra tartás egyenletességének jellemzéséhez adja meg, hogy a lősorozatban hány 0 körértékű találat volt! (szétszórt :l)
- A lövész teljesítményét jellemzi, ha valamelyik irányban több találata van, mint a többiben. Adjuk meg, hogy a nem 0 körértékű találatok közül hány volt az egyes síknegyedekben! Írjuk a képernyőre az eredményeket a következőhöz hasonló formában: "1. síknegyedben: 13 találat, 2. síknegyedben: 18 találat, ..."! (síknegyed :l)
$(x~\ge~0$ és $y~\ge~0~\rightarrow~síknegyed~=~1)$ és
$(x~\ge~0$ és $y~\lt~0~\rightarrow~síknegyed~=~4)$ és
$(x~\lt~0$ és $y~\ge~0~\rightarrow~síknegyed~=~2)$ és
$(x~\lt~0$ és $y~\lt~0~\rightarrow~síknegyed~=~3)$
- Döntsük el, hogy volt-e olyan négy egymás utáni lövés, hogy a találatok az 1., a 2., a 3. és a 4. síknegyedbe csapódtak egymás után! (szórt :l)
Rétes
Kiránduláson a hosszú túra után mindenki legfeljebb három rétest kérhet vacsorára a turistaházban. A neveket és választott rétesfajtákat listában tároljuk.
Példa: [[András [mákos meggyes almás]] [Joli [túrós]] [Anna [almás almás]] [Tamás []] [Mari [almás meggyes]] [Vera []]]
Minta bemenet:
eljárás osztály
eredmény [
[András [mákos meggyes almás]]
[Joli [túrós]]
[Anna [almás almás]]
[Tamás []]
[Mari [almás meggyes]]
[Vera []]
]
vége
- Ki nem kért egyetlen rétest sem?
Példa: nemeszik osztály Eredmény: [Tamás Vera]
- Adjuk meg, hogy ki hány rétest kért!
Példa: kérés osztály Eredmény: [[András 3] [Joli 1] [Anna 2] [Tamás 0] [Mari 2] [Vera 0]]
- Milyen fajta rétest kérnek a gyerekek? Minden fajta egyszer szerepeljen a listában!
Példa: rétesfajták osztály Eredmény: [mákos túrós almás meggyes]
- Hány darabot kell rendelni az egyes rétesfajtákból?
Példa: rétesszámok osztály Eredmény: [[mákos 1] [túrós 1] [almás 4] [meggyes 2]]
- Határozzuk meg, hogy egyes rétesfajtákat kik kérték!
Példa: fajtakérők osztály Eredmény: [[mákos [András]] [túrós [Joli]] [almás [András Anna Mari]] [meggyes [András Mari]]]
Állattenyésztők
(Nemes Tihamér OKSzTV'96 elsőfordulós feladata alapján)
Két állattenyésztõ nyilvántartást vezet állatairól. Ez a nyilvántartás kétszeres mélységű sorozat, amely ábécé szerint rendezve tartalmazza az állatfajták nevét és darabszámát.
Példa:
agazda: [[kacsa 5][liba 13][nyúl 66][tyúk 4]]
bgazda: [[kacsa 1][kecske 33][nyúl 99]]
- Határozzuk meg a két gazda állatainak számát!
Példa: állatszám agazda bgazda Eredmény: 221
- Készítsünk függvényt, amellyel meghatározzuk, hogy az állatfajtákból hány példányuk van együttesen!
Példa: közös agazda bgazda Eredmény: [kacsa 6] [kecske 33] [liba 13] [nyúl 165] [tyúk 4]
- Készítsünk olyan függvényt, amely megadja, hogy a két gazdának összesen hány fajta állata van!
Példa: fajtaszám agazda bgazda Eredmény: 5
- Készítsünk olyan függvényt, amely megadja, hogy melyik állatfajtából mennyit tudnak eladni akkor, ha egy-egy állatfajtából mindkettőjüknek ugyanannyit kell értékesíteniük!
Példa: eladhatók agazda bgazda Eredmény: [kacsa 1] [nyúl 66]
- Készítsünk olyan függvényt, amely megadja, hogy hány olyan állatfajta van, amely csak egyik gazdá-nak van!
Példa: különbözők agazda bgazda Eredmény: 3
Szülő-gyerek kapcsolat
Adott szülő-gyerek kapcsolatpárok sorozata. Például, ha az 1. ember szülője a 2.-nak, a 2. pedig a 3.-nak, akkor a sorozat: [[1 2][2 3]]. Feltesszük, hogy mindenkinek maximum 2 szülője lehet.
- Határozzuk meg a bemenő listából az összes szülőt! Minden szülő csak egyszer szerepeljen az eredményben.
Példa: szülők kapcsolat Eredmény: [1 2 6 7 8 10 13 14 16 18]
- Készítsünk függvényt, amely megadja minden szülő gyerekeit!
Példa: gyerekeik kapcsolat Eredmény: [[1 [2 3 4]] [2 [5]] [6 [2]] [7 [3 4]] [8 [9]] [10 [11 12]] [13 [11 12]] [14 [15]] [16 [15 17]] [18 [17]]]
- Adjuk meg minden szülőhöz a gyerekeik számát!
Példa: gyerekszámok kapcsolat Eredmény: [[1 3] [2 1] [6 1] [7 2] [8 1] [10 2] [13 2] [14 1] [16 2] [18 1]]
- Adjuk meg minden szülő esetében, hogy a gyerekeiknek kik a másik szülei!
Példa: társak kapcsolat Eredmény: [[1 [6 7 7]] [2 []] [6 [1]] [7 [1 1]] [8 []] [10 [13 13]] [13 [10 10]] [14 [16]] [16 [14 18]] [18 [16]]]
Dominó
Minden dominó két nem negatív egész számból, illetve annak megfelelő számú pöttyből áll.
A dominókészlet méretét az adja, hogy mennyi a maximális szám, ami egy dominón van. Egy N nagyságú készletben minden szám 0 és N közötti. Két dominó megegyezik, ha rajtuk a számok megegyeznek, az olvasási sorrendtől függetlenül. Egy dominókészlet nem tartalmaz azonos dominókat.
Egy 2-es méretű dominó készlet a következő dominókat tartalmazza: [0 0] [0 1] [0 2] [1 1] [1 2] [2 2]
- Állítsunk elő N méretű dominókészletet!
Példa: dominó 3 Eredmény: [[0 0] [0 1] [0 2] [0 3] [1 1] [1 2] [1 3] [2 2] [2 3] [3 3]]
- Készítsünk függvényt, amely egy N nagyságú dominókészlet összes pöttyeinek számát adja meg!
Példa:
pöttyszám 2 Eredmény: 12
pöttyszám 3 Eredmény: 30
- Állítsunk elő véletlenszerűen adott számú dominót, N nagyságú készletből (húzás :n :db)! A dominók ismétlődése nem megengedett. A paraméterek helyességét nem kell ellenőrizni!
Példa: húzás 3 5 Eredmény: [[0 2] [2 2] [0 0] [1 1] [1 2]]
- Próbáljunk meg kirakni szabályosan egy adott dominósorozatot!
Szabályok:
- csak a sorozat első dominóját tehetjük az eddigi részmegoldáshoz,
- az „érintkező” számoknak azonosnak kell lenni,
- az első dominót megfordíthatjuk, azaz a számait felcserélhetjük (így is írjuk ki),
- a részmegoldás-sorozat mind a két végéhez tehetjük a dominót,
- ha a részmegoldás egyik végéhez sem tudjuk tenni a soron következő dominót, akkor írjuk ki, hogy „Részben rakható ki”!
Példa:
játék [[3 3] [0 3] [1 3] [0 1] [1 1]] Eredmény: [[1 1] [1 0] [0 3] [3 3] [3 1]]
játék [[0 2] [2 2] [0 0] [1 1] [1 2]] Eredmény: [Részben rakható ki: [0 0] [0 2] [2 2]]
Rendezés bináris fával
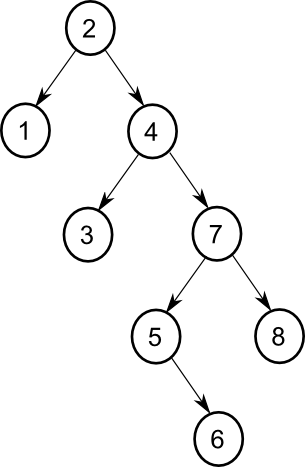
A bináris fa olyan, hogy a gyökérből kiágazó baloldali részfa csupa olyan elemet tartalmaz, amely kisebb, vagy egyenlő az aktuális gyökérnél. A jobboldali részfa pedig csupa olyan elemet tartalmaz, amely nagyobb az aktuális gyökérben lévő elemnél. A bináris fa BKJ-bejárása a számok rendezett sorrendjét adja.
Építsük fel a bináris fát az adott elemekből és adjuk meg a rendezett sorrendet!
Példa: rendezés [2 4 7 1 5 3 6 8] Eredmény: [1 2 3 4 5 6 7 8]
A lista szerkezete elemenkénti beillesztéssel
| 1. | [2] |
| 2. | [2 [4]] |
| 3. | [2 [4 [7]]] |
| 4. | [[1] 2 [4 [7]]] |
| 5. | [[1] 2 [4 [[5] 7]]] |
| 6. | [[1] 2 [[3] 4 [[5] 7]]] |
| 7. | [[1] 2 [[3] 4 [[5 [6]] 7]]] |
| 8. | [[1] 2 [[3] 4 [[5 [6]] 7 [8]]]] |