Dolgozat
1. feladat
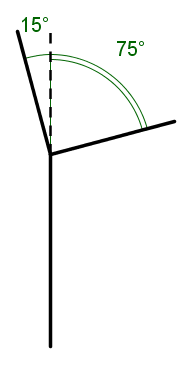
Készíts FA :H :N eljárást a bináris fa kirajzolásához. Az elágazás után a hossz 2/3-a az elágazás előttinek. A :H paraméter az első vonal hossza, :N pedig a szintek száma. Az ábrán látható fa szintszáma 2.
Megoldás
Zsakó András kódja alapján
eljárás FA :H :N
ELŐRE :H
HA :N>1
[BALRA 15 FA :H/2 :N-1
JOBBRA 90 FA :H/2 :N-1
BALRA 75]
HÁTRA :H
vége
2. feladat
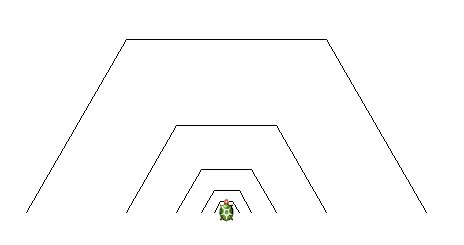
Készíts TRAP :H :N eljárást az ábrához. :H a legnagyobb trapéz szárának hossza, :N pedig a trapézok száma. Az ábra befelé "fejlődik", minden újabb trapéz fele akkora, mint az előző.
Megoldás
Holocsi Szilvi kódja alapján
eljárás TRAP :h :n
TF b 90 E :h TL
J 120 E :h
J 60 E :h
J 60 E :h
TF J 120 E :h J 90
HA :n > 1 [TRAP :h/2 :n-1]
vége
3. feladat
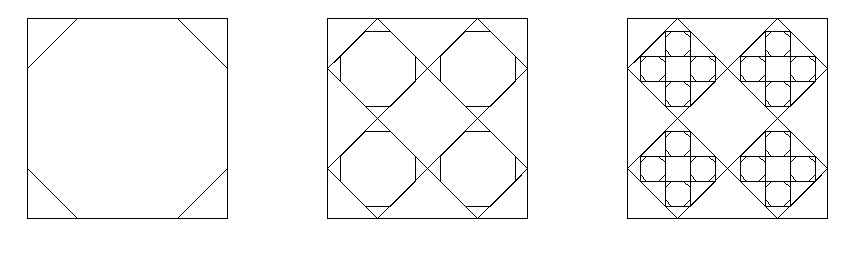
Írj rekurzív NEGY :H :N eljárást az alábbi rajzok elkészítéséhez. :H a legnagyobb négyzet oldalhossza, az ábrák az :N=1, :N=2, :N=3 eseteket mutatják.
Megoldás
Mohos Péter Pál kódja alapján
eljárás negy :h :n
ism 4 [e :h/4 j 135 e (gyök 2)*(:h/4) j 135 e :h/4 j 90 e :h j 90]
ha :n>1
[
e :h/4
ism 4 [
tf e :h/4*3 j 90 e :h/4 j 45 tl
negy (gyök 2)*(:h/4) :n-1 b 45
]
h :h/4
]
vége
Bágyoni Attila kódja alapján
eljárás NEGY :H :N
HAK :N>1
[
E :H/4
J 45 NEGY :H/4 * gyök 2 :N-1
B 90 NEGY :H/4 * gyök 2 :N-1
ISM 2 [j 90 e :H/4 * gyök 2]
B 90 NEGY :H/4 * gyök 2 :N-1
ISM 2 [j 90 e :H/4 * gyök 2]
B 90 NEGY :H/4 * gyök 2 :N-1
J 90 E :H/4 * gyök 2
J 45 E :H*3/4 ISM 5 [J 90 E :H]
]
[
ISM 4 [E :H J 90]
E :H*3/4 J 45 E :H/4 * gyök 2 J 45
ISM 3 [E :H/2 J 45 E :H/4 * gyök 2 J 45]
E :H*3/4
]
vége
Albini Valentin kódja alapján
eljárás negy :h :n
ism 4 [ e :h j 90 ]
e :h/4
ism 4 [e :h/2 j 45 e (gyök 2)*:h/4 j 45 ]
h :h/4
ha :n>1
[
e :h/4 j 45
negy (:h/4)*(gyök 2) :n-1
b 45 e :h/2 j 45
negy (:h/4)*(gyök 2) :n-1
e (gyök 2)*:h/4 j 45 e :h/2 j 45
negy (:h/4)*(gyök 2) :n-1
e (gyök 2)*:h/4 j 45 e :h/2 j 45
negy (:h/4)*(gyök 2) :n-1
e (gyök 2)*:h/4 j 45 e :h*3/4 j 90
]
vége