A megoldás algoritmusa
A minimális költségű feszítőfa kereséséhez egy már ismert módszer, a Kruskal algoritmus segíti munkánkat. Az algoritmus vázlata így szól:
- Vesszük a gráf összes csúcsát, élek nélkül.
- Megnézzük, hogy az elhagyottak közül melyik a legkisebb költségű él.
- Ha a kiválasztott él felvételével nem keletkezik kör a gráfban, felvesszük. (Az első élnél triviális.) Ha viszont kör keletkezne, nem vesszük fel.
- Ha a gráf még nem összefüggő és van még él, megkeressük a következő legkisebb költségű élt, majd visszatérünk az előző pontra.
Az előbbi algoritmus véges lépés után befejeződik, mivel véges sok él van. Továbbá, mivel a feladatban szereplő gráf összefüggő, így végeredményként egy körmentes, összefüggő gráfot kapunk, amely a gráf minimális költségű feszítőfája.
Az algorimus kicsit átalakítva így szól pszeudokódban:
Rendezzünk az éleket költség szerint növekvő sorrendben
Ciklus amíg nem fa és van még él
Vesszük a következő élt a rendezett listában
Ha nincs út az él két végpontja között akkor
Felvesszük az élt
Elágazás vége
Ciklus vége
Egyszerű, ugye? Ugyanis ha egy él felvételével kört tartalmazna egy gráf, akkor az él két végpontja között útnak kell lennie.
Ez egy mohó algoritmus, mivel mindig az adott legjobb lépést választja, ami nem garantálja a végső optimális megoldást. De vajon miért is lesz helyes az algoritmus?
Az algoritmus helyességének bizonyítása
Ez a fejezet pusztán érdekességként szolgál. Megértésével okosodik az olvasó elméje, de a kódoláshoz nem szükséges az ismerete.
A problémát indukciós úton bizonyítjuk. Mint már láttuk, az első él felvételével nem keletkezik kör a gráfban (triviális). Tegyük fel, hogy n él felvétele után optimális megoldást kapunk az algoritmus használatával, azaz létezik olyan minimális költségű feszítőfa (F), melynek részgráfja az algoritmussal kapott (nem összefüggő) gráf.
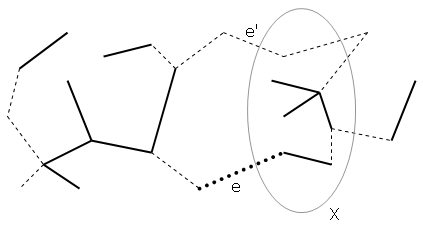
Vegyük fel a következő élt (továbbiakban e) az algoritmusunk szerint. Ha e élt tartalmazza F, akkor készen vagyunk, mivel F összes részgráfja is optimális. Ellenkező esetben F feszítőfa e-t nem, de az összes eddig felvett élt tartalmazza. Továbbá bontsuk szét az eddigi gráfot két részgráfra (X és X') úgy, hogy a kettőt csak e él kösse össze az eddigiekben felvett élek közül.
Világos, hogy ha e-t behúznánk az F fában, kört kapnánk. Mivel e összeköti a két halmazt, és F egy útja összeköti e két végpontját, ezért létezik olyan él F-ben (e'), amely a két részhalmaz között halad. e'-nek nem lehet kisebb a költége e-nél, mivel az algoritmus szerint e'-t vettük volna fel e helyett. Azonban nagyobb sem lehet a költsége, mivel F gráfban e' elhagyásával és e felvételével ugyancsak feszítőfát kapnánk, melynek költsége kisebb lenne F költségénél. Ez nem lehetséges, mivel F feszítőfa optimális volt. Így arra jutottunk, hogy e és e' költségei megegyeznek, vagyis e él felvételével ugyanolyan optimális gráfot kapnánk, mintha e'-t vennénk fel.
Bebizonyítottuk tehát, hogy az algoritmussal az n+1-edik él felvétele is optimális megoldáshoz vezet, vagyis az algorimus (mohó volta ellenére) helyesnek bizonyult.
Út keresése
...
Megoldások