6. óra
Az óra anyaga
Ezen az órán azt a nagyobb célt tűztük ki, hogy írunk egy útvesztő-készítő programot. Először is konkrétabban meg kell fogalmazni a feladatot.
Specifikáció
Legyen egy útvesztő egy olyan négyzetrács, amiben átjárható és fal mezők vannak, illetve egy start és egy cél. A start és a cél helye lehet rögzített pl. bal-felső és jobb alsó sarkok. Kikötjük még azt is, hogy az útvesztő bármely két átjárható mezője közt csak egyetlen útvonal lehet. (Tehát nem tartalmazhat kört, útvonal az átjárható mezők sorozata. Csak az éllel való érintkezés számít.) Például a következő ábrán az X falat jelez, a szóköz átjárható mezőt, a két * pedig a start és a cél. Tehát a következő példához hasonló útvesztőket szeretnénk előállítani:
Azt szeretnénk, ha programunknak meg lehetne adni az útvesztő szélességét és magasságát is. A szélesség legyen a karakterek vízszintes száma, a magasság pedig a függőleges. Az előbbi képen például a magasság 13 karakter a szélesség pedig 23 karakter. Ugyan még nem biztos, hogy minden kérdést tökéletesen precízen tisztáztunk, de ennyi már elég ahhoz, hogy elkezdhessük a tervezést.
Tervezés, részekre bontás
Az algoritmus
Paja ötlete alapján.
Induljunk ki az ábrán látható négyzetrácsból! Ez a négyzetrács igazából tekinthető egy egyszerű útvesztőnek: a kék vonalakon lehet csak menni, a piros körből kell indulni, és a kék csúcsba kell érkezni. (Most még sokféleképpen át lehet rajta menni.) Viszont ebből a rácsból kiindulva már készíthetünk egy valódi útvesztőt is. A vonalak kereszteződéseit csúcsoknak fogjuk nevezni, két szomszédos csúcs közti utat pedig élnek. (pl. a két zöld kör közti vonal egy él, a zöld körök pedig egy-egy csúcsot fednek le) Vegyük sorra az összes élet, véletlenszerű sorrendben. Ha elérkezünk egyhez, nézzük meg, hogy ha kitörölnénk, akkor a két végpontja között még mindig maradna-e út (más élek sorozata). Ha igen, akkor töröljük ki az adott élet, egyébként hagyjuk meg! A két zöld csúcs közötti élet például nyugodtan kitörölhetjük. (Mivel az első néhány lépésben bármelyik út kitörölhető.) Néhány lépés után eljuthatunk egy ehhez hasonló ábrához:
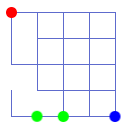
Itt például már nem lehet kitörölni a két zöld csúcs közötti élet, mert akkor nem maradna köztük út. Más szóval, a gráf két komponensre esne. Ha végigmentünk így az összes élen, akkor a maradék élek már egy valóban jó útvesztőt fognak alkotni. Ugyanis vigyáztunk rá, hogy bármely két szomszédos csúcs között maradjon út, és ebből következik, hogy bármely két tetszőleges csúcs között is maradni fog út. Ráadásul pontosan egy út fog csak maradni: tegyük fel, hogy maradt két csúcs, amik között két különböző út is mehet. Ez nem lehetséges, mert az algoritmusunk, amikor elért a két út valamelyikének egy éléhez, akkor azt kitörölte volna.
Tárolás a memóiában
A következő feladat az, hogy tudjunk ilyen rácshálóból készített útvesztőket memóriában tárolni és módosítani, az algoritmus megvalósításához. Aztán pedig az, hogy ezeket a specifikációban megadott karakteres formára alakítsuk. Az egyik lehetőség az, hogy valamilyen gráf-ábrázolási módszerrel tároljuk el a rácsot. Ekkor viszont külön kellene tárolni a csúcsok és élek síkbeli elrendezését, ezért inkább egy másik módszert alkalmazunk. Alakítsuk át útvesztőnket egy olyan négyzetráccsá, amiben a "fehér" négyzeteken át lehet haladni, a "feketéken" meg nem! Ehhez leteszünk egy kétszeres sűrűségű másik rácsot, és ennek a rácsnak azokat a mezőit színezzük be "feketére", amikben az útvesztőnek nincs sem útja, sem kereszteződése.
Ugyanez egy kész útvesztőre:
Vegyük észre, hogy bizonyos mezők mindig falak lesznek, bizonyos mezők pedig sosem lehetnek azok. A következő ábrán szürkével jelöltek mindig falak lesznek. A zöld kettes mező az eredeti útvesztőben egy csúcs volt, tehát sosem lesz fal. A zöld egyes pedig egy él volt, tehát néha fal lesz, néha meg nem, attól függően, hogy az algoritmus kihúzta-e az adott élet. Az ilyeneket majd él típusú mezőknek, vagy él-mezőknek fogjuk hívni.
Az útvesztőt ennek a négyzetrácsnak például egy N-szer M-es Igaz-Hamis (logikai) tömb reprezentációjában tárolhatjuk. Tehát, ha pl. map[sor, oszlop] = Igaz, akkor ott szürke négyzet (fal) van, ha Hamis, akkor pedig fehér négyzet. N-et és M-et mindig páratlannak érdemes megválasztani, különben a pálya szélein kis, egy hosszú leágazások maradhatnak.
Első Részfeladat: Útkeresés
Algoritmusunkhoz szükség lesz egy olyan függvényre, ami eldönti két csúcs típusú mezőről, hogy van-e köztük út. (Csúcs típusú, ami az eredeti rácsban csúcs volt.) Az egyszerűség kedvéért egy olyat fogunk írni, ami nem foglalkozik azzal, hogy a mező csúcs vagy él volt eredetileg, hanem csak azt veszi figyelembe, hogy átjárható, vagy fal-e. A függvény legyen a következő alakú: Függvény Ut(sor1, oszlop1, sor2, oszlop2): Logikai. Akkor térjen vissza Igaz-al, ha a [sor1, oszlop1] és a [sor2, oszlop2] koordináták között van út.
Tesztelési környezet
Először írjunk meg néhány egyszerű eljárást, amikkel majd tesztelni lehet függvényünket : legyen N és M rögzített pozitív egyész konstans, és legyen map[1..n, 1..M] Igaz-Hamis értékek tömbje. Legyen az Igaz az átjárható mező, a Hamis pedig a fal! A következő módon véletlenszerű térképeket fogunk csinálni a teszteléshez:
Eljárás VTerkep()
Ciklus sor:= 1-től N-ig
Ciklus oszlop:= 1-től M-ig
map[sor, oszlop]:= Veletlen() > 0.5;
Ciklus vége
Ciklus vée
Eljárás vége
A Veletlen() függvény egy 0 és 1 közti véletlenszámot ad eredményül. A Veletlen() > 0.5 egy logikai kifejezés, ami Igaz vagy Hamis értéket ad vissza. Ne felejtkezzünk el a véletlenszám-generátor inicializálásáról!
Érdemes írni egy olyan függvényt is, ami megjeleníti az elkészült térképet.
Eljárás Kirajzol()
Ciklus sor:= 1-től N-ig
Ciklus oszlop:= 1-től M-ig
Ha map[sor, oszlop] = Igaz Akkor
Kiir(' ');
Különben
Kiir('#');
Ciklus vége
Kiir(újsor);
Ciklus vége
Eljárás vége
Ezek után esetleg a 0.5-ös fal/átjárható mező arányt is megváltoztathatjuk, hogy a tesztelésre alkalmasabb térképeket készítsünk!
Az útkereső algoritmus
Egy nagyon egyszerű útkereső algoritmust fogunk megvalósítani. Legyen S a kiindulási pont, C pedig a cél. Kezdetben minden átjárható pont a térképen fehér. Első körben színezzük be S-et pirosra. Az algoritmus a következő lépés ismételgetéséből fog állni: megkeresi az összes piros mezőt, és minden átjárható szomszédjukat is pirosra festi. Ezt addig kell ismételgetni, amíg vagy C is piros lesz (ilyenkor van út), vagy nem találunk újabb pirosra festhető mezőket, mert S el van kerítve C-től, tehát nincs út. Valójában az S-ből úttal elérhető mezőket festettük pirosra...
Szükségünk lesz egy tömbre, a piros mezők tárolásához, pl.: red[sor, oszlop]. Kezdetben minden mezője hamis legyen.
Eljárás Ut(sor1, oszlop1, sor2, oszlop2) : Logikai
red[sor1, oszlop1]:= Igaz;
volt:= Hamis;
Ciklus Amíg (volt = Hamis) és (red[sor2, oszlop2] = Hamis)
volt:= Hamis;
Ciklus sor:= 1-től N-ig
Ciklus oszlop:= 1-től M-ig
Ha red[sor, oszlop] = Igaz Akkor
Ha (map[sor+1, oszlop] = Igaz) és
(red[sor+1, oszlop] = Hamis) Akkor
red[sor+1, oszlop]:= Igaz;
volt:= Igaz;
Elágazás vége
Elágazás vége
Ciklus vége
Ciklus vége
Ciklus Vége
Ut:= piros[sor2, oszlop2];
Eljárás vége
Ha a volt értéke Hamis marad egy ciklusban, az azt jeletni, hogy minden piros mezőnek vagy pirosak, vagy falak a szomszédai, tehát az S-ből elérhető mezők (a piros zóna) nem bővíthető tovább. A négy szomszédot ugyanúgy kell kezelni, úgyhogy írhatunk rájuk egy közös eljárást. Ebből a mintából hiányzik a tömb szélének az ellenőrzése. Kétféle képpen lehetne megcsinálni: vagy mind a négy szomszédnál ellenőrzéseket írunk a koordinátákra, vagy megnöveljük a map és red tömböket, hogy a méretük 0..N+1-szer 0..M+1 legyen, és a szélére fal mezőket rakunk. A második módszer egyszerűbb és gyorsabb, ráadásul ilyen kis méreteknél nem érdemes a memóriával spórolni.
A teszteléshez érdemes írni egy olyan Kirajzol() eljárást is, ami a piros mezők helyett pl. egy *-ot jelenít meg.
Megjegyzések
-
Ennél az algoritmusnál lehetséges hatékonyabb útkereséseket is írni, de ezt a legkönnyebb gyorsan leprogramozni, és a középiskolás (országos) versenyeken legtöbbször ez is elég. A futási ideje felülről becsülhető N*M*N*M lépéssel. Ugyanis minden tömb-végigsöpréssel legalább egy mezőt pirosra festünk, és legfeljebb N*M mezőt kell pirosra festenünk.
-
A hibakeresés közben ne lepődjünk meg, hogy egy körben nem csak az adott piros mezők szomszédai változnak pirosra, hanem helyenként egy nagyobb környezetük is, a bejárás iránya szerint.
Megoldások
Folytatás



 ->
-> ->
-> ->
->
 ->
-> ->
-> ->
->

